Download let g be cyclic group of order n then a_k is generator of g if gcd(k, n)=1 MP3 & MP4 You can download the song let g be cyclic group of order n then a_k is generator of g if gcd(k, n)=1 for free at MetroLagu. To see details of the let g be cyclic group of order n then a_k is generator of g if gcd(k, n)=1 song, click on the appropriate title, then the download link for let g be cyclic group of order n then a_k is generator of g if gcd(k, n)=1 is on the next page.

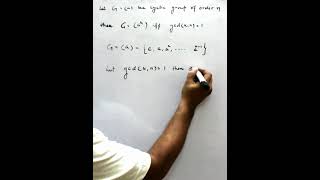	Let G be cyclic group of order n then a k is generator of G if gcd(k, n)=1 (Roman Education Roman vocabulary) View
	a^(m) is a generator of group G of order n iff GCD(m,n)=1 (Maths ICU) View
	Let G be cyclic group and a is it's generator. The element a^k is also a generator iff ( k,d)=1 (Shahanaj S K) View
	Abstract Algebra - 4.2 Cyclic Groups and Their Properties a^k=a^gcd(n,k) (Kimberly Brehm) View
	[a^k] = [a^gcd(n,k)] and \|a^k\| = n/gcd(n,k) Proof (Abstract Algebra) (BriTheMathGuy) View
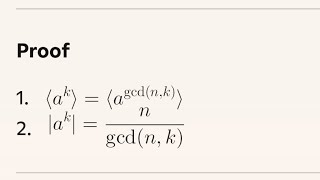$Download Lagu proof.{a^k}={a^gcd(n,k)} and \|a^k\|=n/gcd(n,k)$	proof.{a^k}={a^gcd(n,k)} and \|a^k\|=n/gcd(n,k) (Uneeb Awais) View
	Math 706 Section 4.1a (Todd Cochrane) View
	Cyclic groups 4 (Jacob White) View
	Let G be group, a ɛ G and O(a)=n. Then for any positive integer k, O(a^k) =n/(n,k). (MathsMentorVishal) View
	Cyclic Groups (Andrew Misseldine) View